N-Queens Part 2: More Algorithms

Last time we were considering the following n-queens board with a current heuristic cost of 5: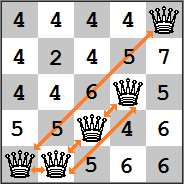By making just one move, the best decision would be to move the second queen to the space marked 2. However, to find that move, we had to go through a somewhat expensive algorithm that checks every possible square. What if instead of trying to find the best move at every step, we simply tried to find a better move?

This method of hill climbing is called first-choice hill climbing. Its implementation is simpler than the steepest-hill method:

def make_move_first_choice(board):
	h_to_beat = get_h_cost(board)
	for col in range(len(board)):	
		for row in range(len(board)):
			if board[col] == row:
				#We don't need to evaluate the current
				#position, we already know the h-value
				continue
			
			board_copy = list(board)
			#Move the queen to the new row
			board_copy[col] = row
			new_h_cost = get_h_cost(board_copy)
			
			#Return the first better (not best!) match you find
			if new_h_cost < h_to_beat:
				board[col] = row
				return board
	
	return board

A final algorithm to consider introduces randomness. Since any n-queens state can be reached from any other n-queens state, it is possible that a solution could arise by simply making random moves. However, a purely random algorithm would take a very long time to stumble upon a solution. The annealing algorithm attempts to tease out the correct solution by making risky moves at first and slowly making more conservative moves.

The algorithm builds on the metaphor of real life annealing, a process used in glass blowing and metallurgy. For example, molten glass is extremely hot, but cools fairly quickly. Generally, room temperature is too cold and the glass will end up cracking. To prevent this, glass is placed into an annealing oven that slowly lowers the temperature, ensuring a more stable cooling process. The algorithm uses a “temperature” and “annealing rate” to “cool” the risk. Here is the basic process:

1. Make a random move
2. If the move results in a lower heuristic cost, accept the move. Otherwise, asses the risk and determine if it should be accepted. If the move is too risky, reject it, and repeat steps 1 and 2.
3. Reduce the temperature by a given annealing rate.
4. Repeat until a solution is found.

Risk is determined using the following:

Given:

• ΔE = current heuristic cost – new heuristic cost
• current temperature T

The probability of acceptance is min(1,e(ΔE/T)).

Much research has gone into determine the correct numbers to use for these variables, but we can use some basic principles for a simple problem like n-queens. In general, you want to start with a high enough temperature that aims for about 80% acceptance on the first move, and you want to anneal at a rate of about 95%.

import math
import random

def annealing(board):
	temp = len(board)**2
	anneal_rate = 0.95
	new_h_cost = get_h_cost(board)
	
	while new_h_cost > 0:
		board = make_annealing_move(board,new_h_cost,temp)
		new_h_cost = get_h_cost(board)
		#Make sure temp doesn't get impossibly low
		new_temp = max(temp * anneal_rate,0.01)
		temp = new_temp
		if steps >= 50000:
			break

def make_annealing_move(board,h_to_beat,temp):
	board_copy = list(board)
	found_move = False

	while not found_move:
		board_copy = list(board)
		new_row = random.randint(0,len(board)-1)
		new_col = random.randint(0,len(board)-1)
		board_copy[new_col] = new_row
		new_h_cost = get_h_cost(board_copy)
		if new_h_cost < h_to_beat:
			found_move = True
		else:
			#How bad was the choice?
			delta_e = h_to_beat - new_h_cost
			#Probability can never exceed 1
			accept_probability = min(1,math.exp(delta_e/temp))
			found_move = random.random() <= accept_probability
	
	return board_copy

This algorithm is a little more complex and involves two methods, but follow along with the general steps above and it should start to make sense.

Note that it is possible for both of these algorithms to get “stuck”. This is known as a plateau. Therefore, it is usually a good idea to put a cap on the number of attempts the algorithm can make before giving up. In the annealing algorithm, I allowed a maximum of 50000 iterations.

In the next post we’ll look at how these algorithms actually perform and make some generalizations about when certain algorithms excel.