N-Queens Part 1: Steepest Hill Climbing

The n-queens problem was first invented in the mid 1800s as a puzzle for people to solve in their spare time, but now serves as a good tool for discussing computer search algorithms. In chess, a queen is the only piece that can attack in any direction. The puzzle is to place a number of queens on a board in such a way that no queen is attacking any other. For example:One way we can describe this board is to say it has a heuristic cost of 0, because there are 0 pairs of queens attacking each other. We can then generalize this to say the heuristic cost of a given n-queens board is equal to the number of queens directly or indirectly attacking one another. Consider this 5-queens puzzle. There are 5 pairs of queens attacking each other therefore the heuristic cost of this board is 5. We can calculate the heuristic cost easily if we represent a board as an array where the index is the column and the value is the row. The board above is [0,0,1,2,4].

def get_h_cost(board):
	h = 0
	for i in range(len(board)):
		#Check every column we haven't already checked
		for j in range(i + 1,len(board)):
			#Queens are in the same row
			if board[i] == board[j]:
				h += 1
			#Get the difference between the current column
			#and the check column
			offset = j - i
			#To be a diagonal, the check column value has to be 
			#equal to the current column value +/- the offset
			if board[i] == board[j] - offset 
				or board[i] == board[j] + offset:
				h += 1
		
	return h

To solve this puzzle, we need to take steps to reduce the heuristic cost to zero.

In order to evaluate which moves are best, we can calculate the heuristic cost of the board after one move. This diagram shows the heuristic costs of all possible moves from the current board. For simplicity, we will only move queens up or down in their rows.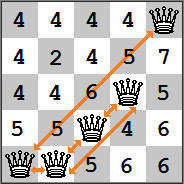 If you would choose the move with the lowest heuristic cost and then repeat the process, then you would be using the steepest hill climbing algorithm.

The hill climbing algorithm gets its name from the metaphor of climbing a hill where the peak is h=0. But there is more than one way to climb a hill. If we always choose the path with the best improvement in heuristic cost then we are using the steepest hill variety.

Steepest hill climbing can be implemented in Python as follows:

def make_move_steepest_hill(board):
	moves = {}
	for col in range(len(board)):
		best_move = board[col]
		
		for row in range(len(board)):
			if board[col] == row:
				#We don't need to evaluate the current
				#position, we already know the h-value
				continue
			
			board_copy = list(board)
			#Move the queen to the new row
			board_copy[col] = row
			moves[(col,row)] = get_h_cost(board_copy)
	
	best_moves = []
	h_to_beat = get_h_cost(board)
	for k,v in moves.iteritems():
		if v < h_to_beat:
			h_to_beat = v
			
	for k,v in moves.iteritems():
		if v == h_to_beat:
			best_moves.append(k)
	
	#Pick a random best move
	if len(best_moves) > 0:
		pick = random.randint(0,len(best_moves) - 1)
		col = best_moves[pick][0]
		row = best_moves[pick][1]
		board[col] = row
	
	return board

But as I mentioned above, there are multiple ways to climb a hill! Next time we’ll look at some additional ways to solve n-queens problems.