In my post last week, I discussed my Java implementation of the MENACE Tic Tac Toe machine. I also mentioned how playing against the MENACE manually is simply too time consuming. And since all programmers are lazy, I of course went on to allow two computer players compete against each other.
However, I never really gave MENACE the best chance for success. Playing against a random computer or another MENACE is really just leaving it up to luck. A successful teacher leads to a more successful student. So I also implemented a computer that plays optimally.
There are a few different ways to do this, and a lot of exercises involve using a minimax algorithm with optional alpha-beta pruning. However, that seems like overkill to me. Tic Tac Toe is a “solved” game meaning that we know how to make the best play every time by simply following a set of rules. Implementing these rules was fairly straight-forward.
So now that MENACE had a good teacher, how long did it take to learn the game? Unfortunately MENACE’s lot in life is sad in that it will never win against an optimal teacher. We know this because a perfectly played game is a draw. So for me the way to determine success is by looking at the optimal player’s wins. The fewer number of times the optimal player wins, the faster MENACE is learning. The mechanics as I found them described online are:
- Win: MENACE gains one bean (+1)
- Draw: MENACE has no change (0)
- Lose: MENACE loses one bean (-1)
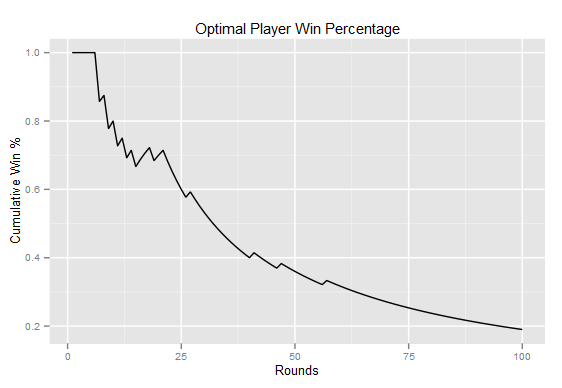
I then ran a simulation of one thousand “tournaments” each consisting of one hundred games. The median number of games the optimal player won was 66. This means on average it took MENACE 66 losses before it could play optimally. This graph shows the cumulative wins the optimal player had in one particular tournament of one-hundred games. The optimal players starts with a 100% winrate, but the winrate slowly drops until the player stops winning all together.
However, I was not convinced that this training method was best. After all, an optimal player should force a draw which means a draw is actually a positive outcome. However, a win is still yet more positive. I tested my theory with a few different values and found these to be the most effective:
- Win: MENACE gains two beans (+2)
- Draw: MENACE gains one bean (+1)
- Lose: MENACE loses one bean (-1)
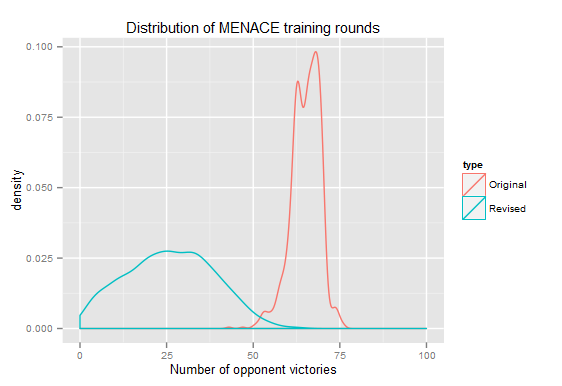
With these values the number of games for optimization was considerably fewer: 26 games. The distribution turned out to be wider mostly because MENACE is more influenced by making lucky or unlucky plays. This graph compares the outcomes of the two tournaments:
This was a fun exploration and there’s still some room for improvement. If you’d like to play with MENACE yourself, the code is available on GitHub.