Restaurants Closer to Columbus’ Population Center are Better

Click to enlarge

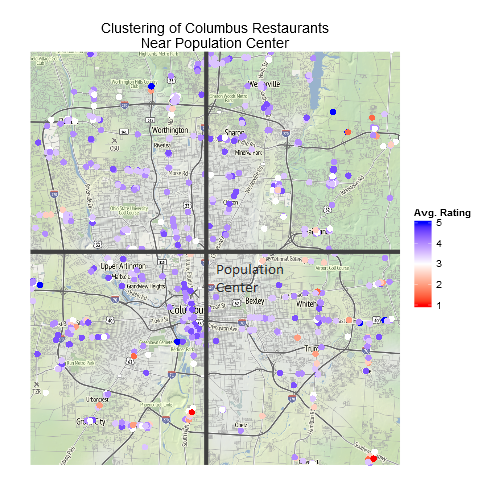
Following my last post on Ohio’s population center, I wanted to get a bit more local. My home town of Columbus has a unique population characteristic: the population is almost uniformly dense. Despite this, I know from personal experience that many of the best restaurants are relatively centrally located in the city. To investigate this further, I used the Yelp API to query information about restaurants in the metro area.

Included in the restaurant details, Yelp provides the latitude and longitude of the restaurant. To find the distance from Columbus’ population center, I used Mario Pineda-Krch’s R implementaion of the Spherical Law of Cosines:

resto<-read.table(".\\data\\restaurants.txt",header=T,sep="\t")
#Exclude restaurants with few ratings
resto<-subset(resto,resto$reviews>2)

oh<-read.table("..\\ColsPop\\data\\data.txt",header=T,sep="\t")
#Arbitrary coordinates the generally bound the Columbus metro area
col<-subset(oh,oh$y < 40.15 & oh$y > 39.85 & oh$x > -83.15 & oh$x < -82.8)
#Note we don't need to correct for longitude
#convergence for small regions
colsCenter <- c(sum(col$num * col$x)/sum(col$num)
				,sum(col$num * col$y)/sum(col$num))

# Calculates the geodesic distance between two points
# specified by radian latitude/longitude using the
# Spherical Law of Cosines (slc)
gcd.slc <- function(long1, lat1, long2, lat2) {
  R <- 6371 # Earth mean radius [km]
  d <- acos(sin(lat1)*sin(lat2) + cos(lat1)*cos(lat2) * cos(long2-long1)) * R
  return(d) # Distance in km
}

deg2rad <- function(deg) return(deg*pi/180)

resto$distToCenter <- gcd.slc(deg2rad(colsCenter[1])
						,deg2rad(colsCenter[2])
						,deg2rad(resto$lon)
						,deg2rad(resto$lat))

My hypothesis was that better-rated restaurants would be closer to the population center. A simple linear model confirmed this: For each kilometer closer to the population center a restaurant can expect about a .03 increase in average rating, significant at p << 0.001. To be clear, this is not a predictive model as there are many other factors that I would expect to more significantly impact a restaurant's rating. Nonetheless, this correlation with centrally is interesting.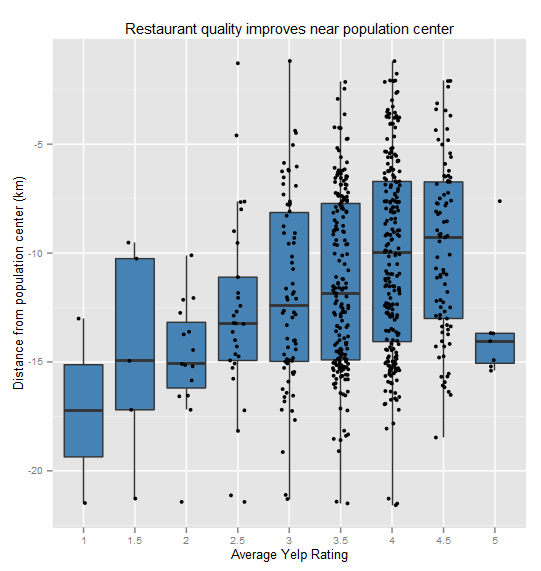Stay tuned for details on using the Yelp API!