N-Queens Part 3: Success
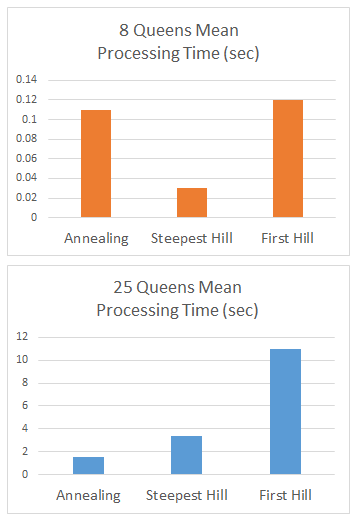
In the last two posts we explored three different algorithms for solving the n-queens problem. If we wanted to actually implement one of them, we would need to consider which one performs the best. However, performance can be measured in a number of ways. The first measurement of performance is simple–how effective is the algorithm at solving the puzzles? Remember that some of the algorithms can get “stuck” and therefore may not reach a heuristic cost of zero. Second we can look at the number of iterations the algorithm takes to solve the puzzle. Finally, the speed of the algorithm should be considered. An ideal algorithm is one that solves the most number of puzzles in the least number of steps and in the least amount of time. In terms of success, both steepest hill climbing and annealing perform equally well (>90%), but first choice hill climbing falls short at only solving approximately 14% of problems. These also hold true regardless of the number of queens. The annealing algorithm takes the most number of steps. This is because as the temperature drops, the algorithm is less likely to accept a move. Therefore, the algorithm takes several steps that do not result in making a move. The steepest hill climbing algorithm takes the fewest number of steps, solving 8 queens in 24 moves and 25 queens in only 35 moves, on average. Measuring performance time is the most interesting because the results scale in an obvious pattern. For 8 queens, the clear winner is the steepest hill algorithm. But if we increase the number of queen, both hill climbing algorithms get much slower, while annealing only gets moderately slower:
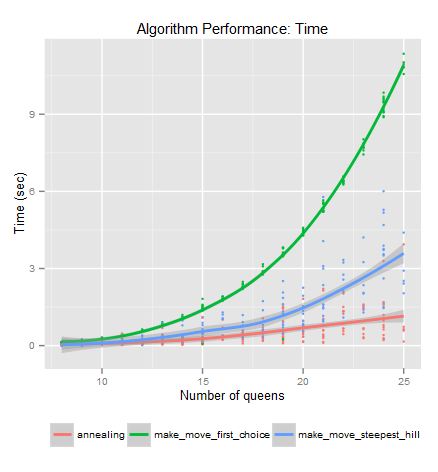
By creating random n-queens puzzles, we can get a very clear picture of how processing time varies with processing time. Consider the following scatterplot:
Clearly, the first hill algorithm becomes increasingly impractical as the number of queens increases. Steepest hill has a less dramatic increase in time, while annealing only has a modest increase. This brief look into some searching algorithms should give you some insight into the many considerations that must be made for actual problem-solving tasks. If you’re interested in learning more, I recommend Russell and Norvig’s Artificial Intelligence: A Modern Approach (Amazon affiliate link). They explore many more related algorithms and delve more into the computer science aspects of algorithms.