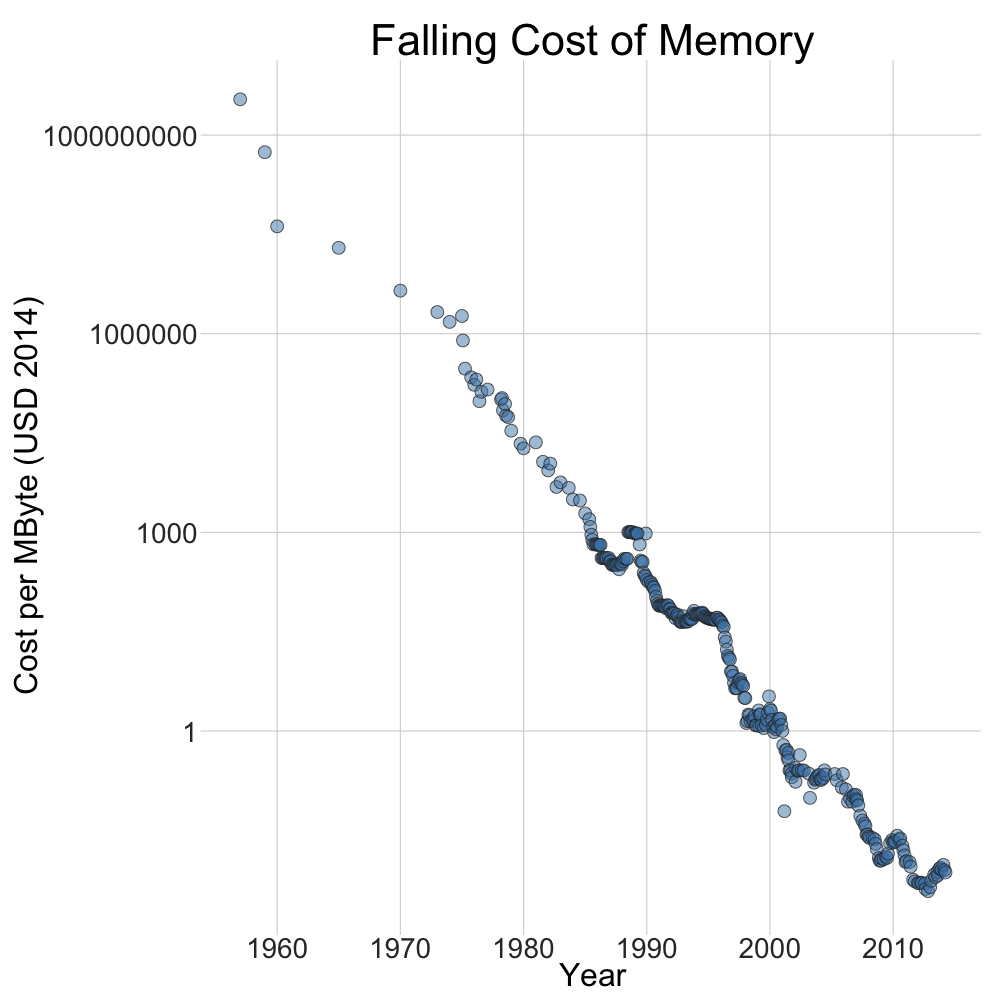
This picture of presidential cat Socks is not what it seems. In addition to being a cat, it also contains the text of the Declaration of the Rights of Man and of the Citizen.
In addition to being a cat, it also contains the text of the Declaration of the Rights of Man and of the Citizen.
By manipulating the image data and the text data at the bit level, we can tweak the image to include information that is imperceptible to the human eye.
Color data in BMP files is stored as RGB values where one byte is allocated for each of red, blue, and green. Each of these values can be changed by a small amount without changing the appearance of the image. To determine what amount to change the bytes by, we use the binary data of the text file.
As an example, let’s see how we would embed the letter “D” into a solid block of orange. The letter “D” has the ASCII hex value 44 and binary value 01000100. The shade of orange I chose has the hex value FF 7F 27 which has the binary value 11111111 01111111 00100111. I mentioned before that we can alter these RGB numbers slightly. The specific method I chose was to set the last bit of each RGB byte to 1 or 0 based on the corresponding bit in the text data. This chart shows how each bit of the “D” is stored across three orange pixels (for a total of 9 bytes–one of which is not used). The orange in the “result” column really is changed. I used the new hex values, but as you can see it looks exactly the same as the “template” column.
The orange in the “result” column really is changed. I used the new hex values, but as you can see it looks exactly the same as the “template” column.
Here is some Python code that will actually do this for us. (Click here for the full script.) First we need to be able to break down the text data into bits:
def data_to_bits(data): bits = [] for i in range(len(data)): #A byte can at max be 8 digits long, i.e. 0b11111111 = 255 #We start at the left most bit (position 7) and work down to 0 for j in range(7,-1,-1): #Create the logic array of bits for our data bits.append(nth_bit_present(data[i],j)) return bits
Then we need a method that will alter an arbitrary byte by setting its last bit to 1 or 0, given a parameter.
def nth_bit_present(my_byte,n): #Bitwise check to see what the nth bit is #If we get anything other than 0, it is TRUE else FALSE return (my_byte & (1 << n)) != 0 def set_final_bit(my_byte,ends_in_one): new_byte = 0 if ends_in_one: if(nth_bit_present(my_byte,0)): new_byte = my_byte #No modification needed, it already ends in one else: new_byte = my_byte + 1 else: if(nth_bit_present(my_byte,0)): new_byte = my_byte - 1 else: new_byte = my_byte #No modification needed, it already ends in zero return new_byte
To extract the “D” from the image, we simply reverse the process. First we extract the final bit from each byte in the image.
with open(sys.argv[1],'rb') as bmp_file:
bmp = bmp_file.read()
#The byte at position 10 tells us where the color data starts
start_offset = bmp[10]
#Deconstruct each byte and get its final bit
bits = []
for i in range(start_offset,len(bmp)):
bits.append(nth_bit_present(bmp[i],0))
And then we can convert a chunk of 8 bits into a byte using some bit shifting.
def bits_to_byte(bits): assert len(bits) == 8 new_byte = 0 for i in range(8): if bits[i]==True: #This bit==1 and the "position" we are at in the byte is 7-i #Bitwise OR will insert a 1 a this position new_byte |= 1 << 7 - i else: #This bit==0 and the "position" we are at in the byte is 7-i #Bitwise OR will insert a 0 a this position new_byte |= 0 << 7 - i return new_byte
By converting all of the “final bits” back into bytes we will have recreated the original text in binary. Using chr(byte) we can get the ASCII value back and print it to the console.
This is a very basic method of steganography that offers some simple obscurity, but not much security. However, if you were to combine steganography with well proven security methods such as encryption, it becomes a powerful tool for hiding data.